電圧と電流を操る?!③
今回は”定格電流を超える”使い方の中で機器定格と実効値の関係について解説します。
電流の実効値
前回お話しました通り、電流の定格は”熱”によって決定されます。しかし、コネクタ選定③で解説した通り、コネクタの定格電圧や電流は各国で使われている電源システムによって定義されています。そのため、各定格は交流電源に基づいて設定されています。
ここで、考えなければならないのが交流での熱と電流の関係です。ジュール熱の計算式は下記でした。
Q = I 2 * R * t (Q: 熱量[J}, I: 電流[A], R: 抵抗[Ω], t: 時間[s])
上記の式において、直流の場合は各係数が一定ですので、計算も簡単です。交流の場合は、ご存知の通り電流 I が時間とともに変動します。
この変動する電流を直流に換算するために、上記の計算式のI 2を計算してみましょう。ここで電流波形の高さを I0 とします。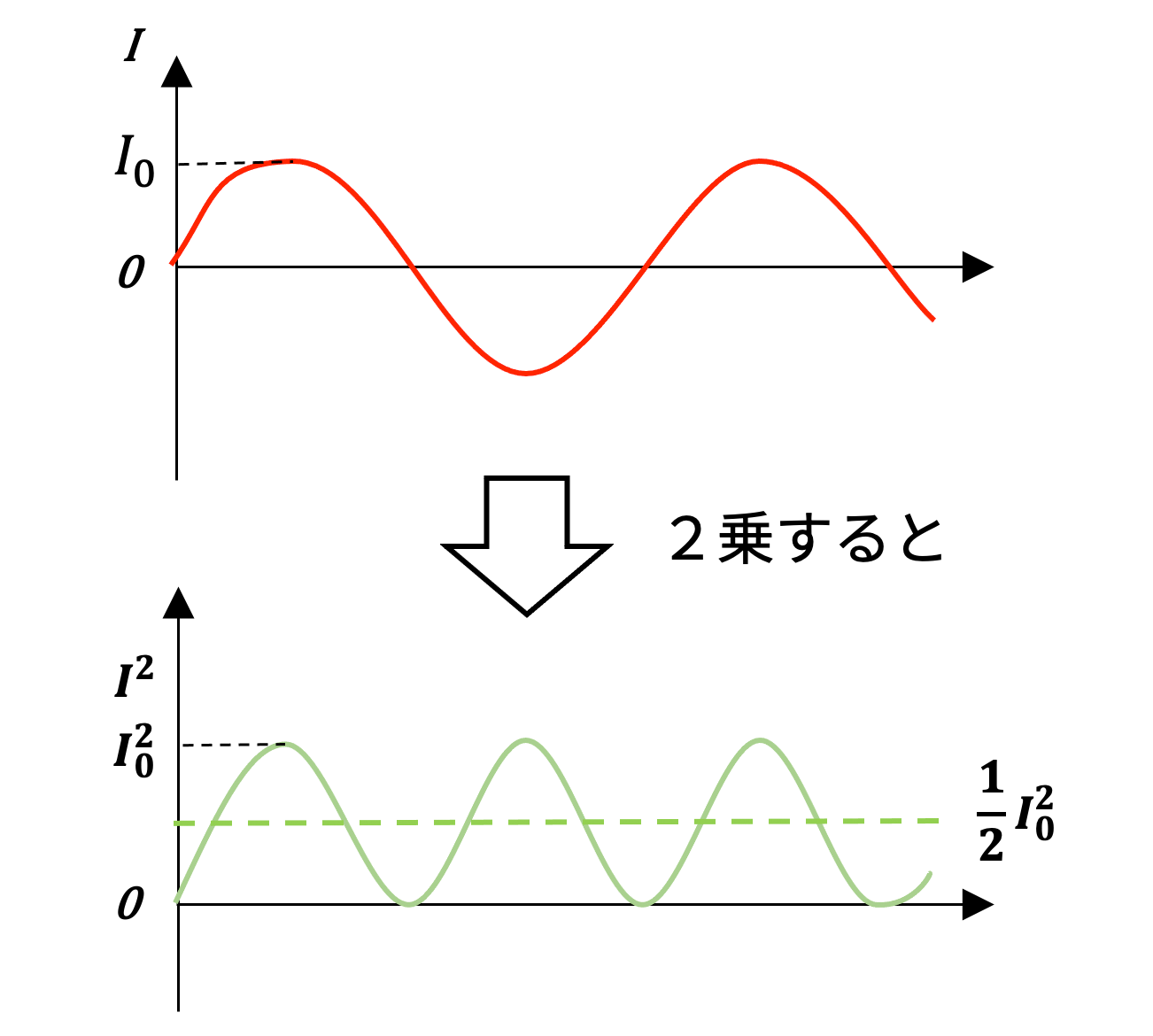
上図のように、2乗するとマイナスがなくなって2倍の周期の波形となりました。
これを直流に換算=フラットな波形にするためには、波形の平均値1/2(上図の点線)で上半分を折り返すことで得ることができます。
ここで少しだけ数学を使いましょう。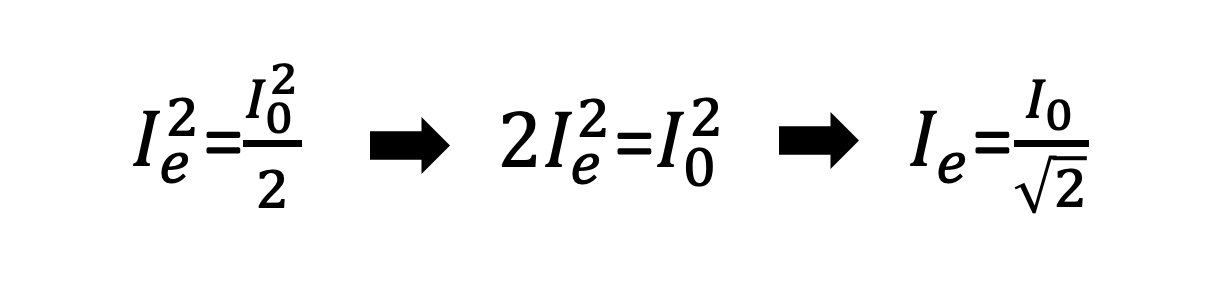
上記のようにフラットな波形を取る電流値Ieは元の波形高さI0の1/√2であることがわかりました。
これを定格電流10Aのコネクタに置き換えると、下記のような関係になります。
定格電流 10A
最大電流(ピーク) 約14.1A (10A x √2)
という事で、瞬間の最大電流は定格電流値よりも大きいことがわかります。
逆にいうと、最大電流が定格電流よりも大きくても、実効値が定格電流以下であれば使用可能ということです。
定格に対する使用可否の判断において実効値の重要性はご理解いただけたと思いますが、商用電源のように正弦波であれば、上記のような計算が簡単にできます。では、ランダムな波形の場合はどうなるでしょうか?
上記で行った、直流に換算=フラットな波形にするは実際には波形の面積に同等な四角形を作っているということになります。
また少し数学が必要になりますが、下記のようなランダムな波形から面積を算出するためには積分を行う必要があります。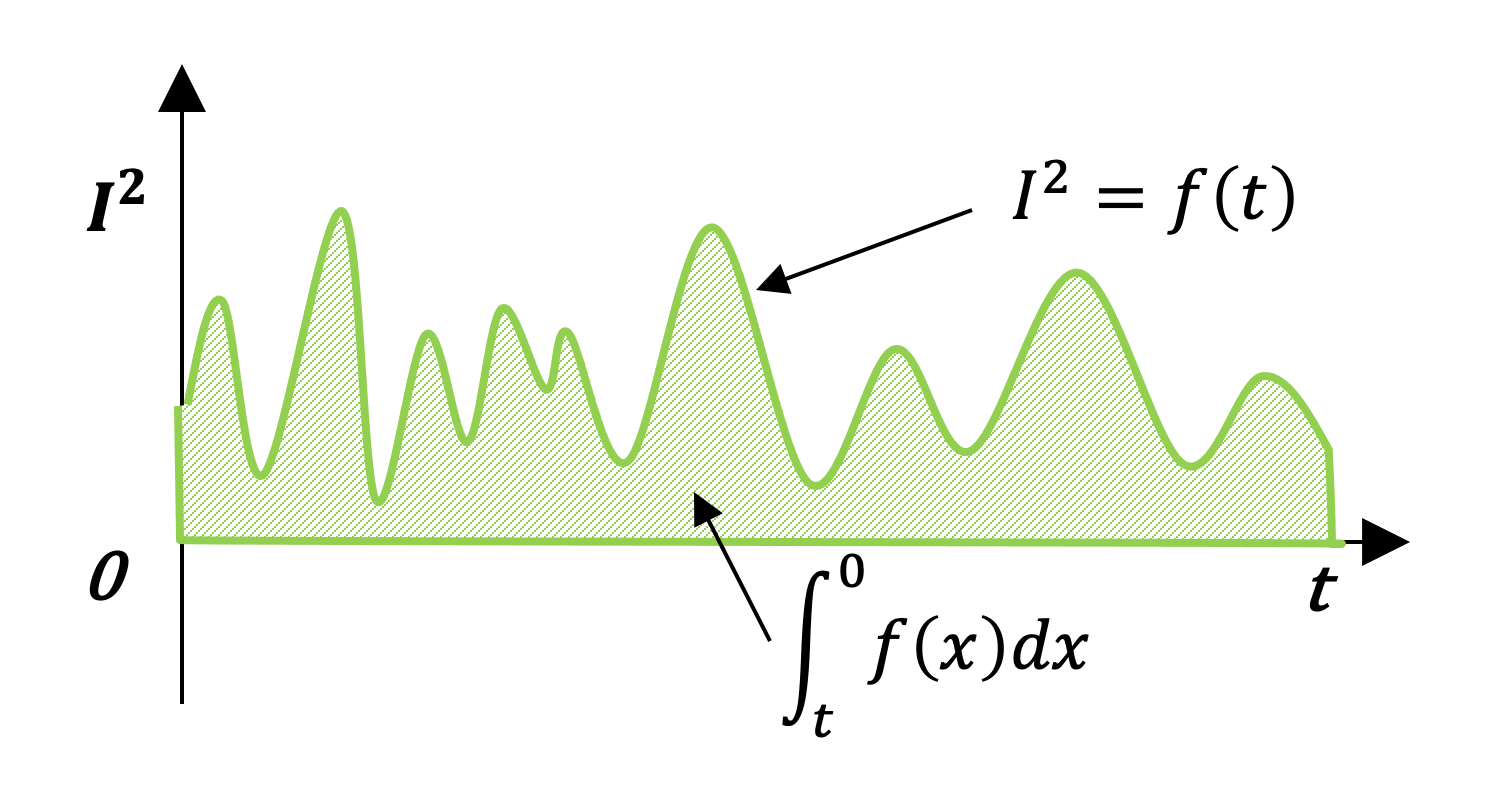
後述しますが、サーボモーターのように電流・周波数が細かく変動するような波形からの実効値を計算するためには、単位時間あたりの平均を積算して面積を算出することになります。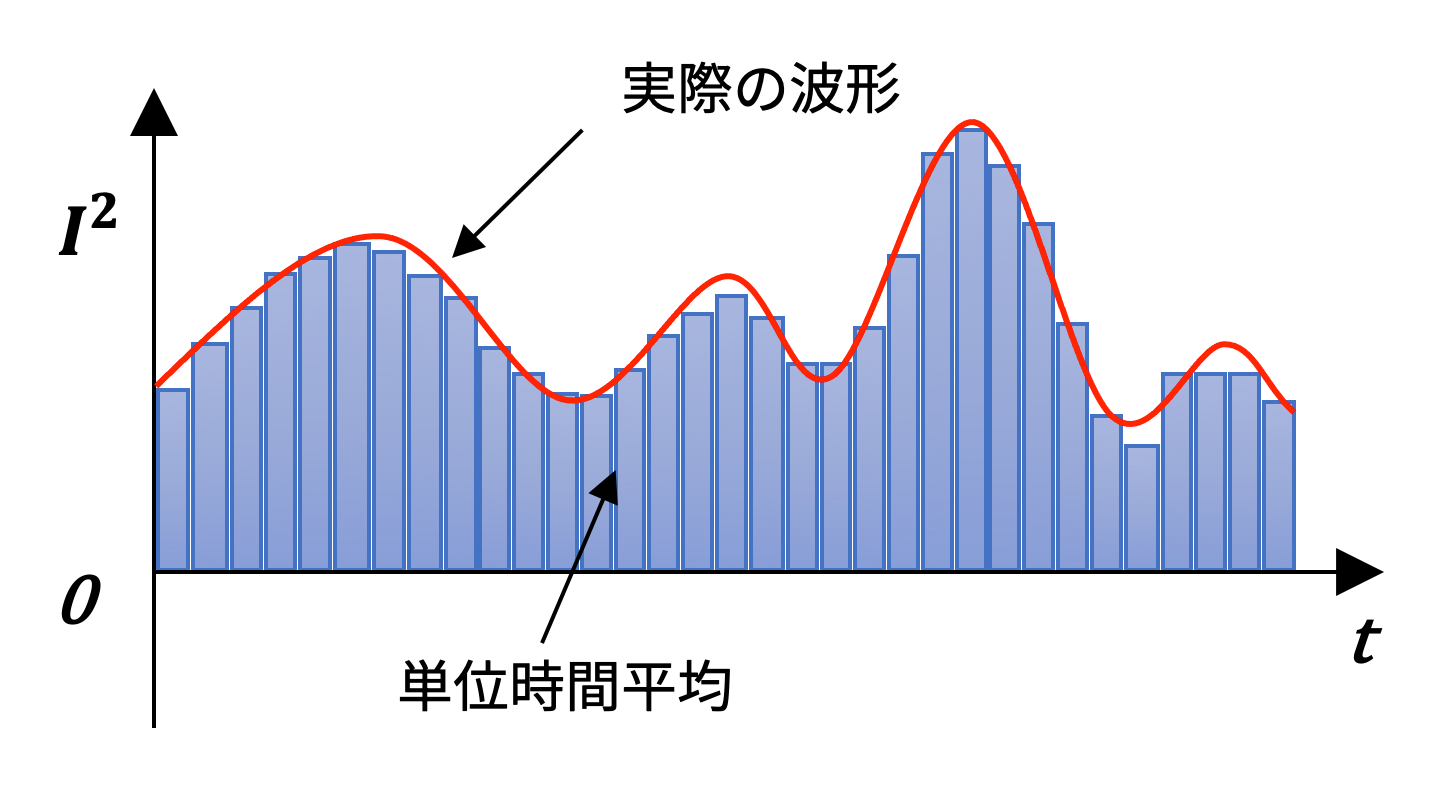
動力の種類と電流波形

すこし実効値の話が長くなりましたが、実際の工場で使われている動力の多くは様々な制御が行われているため、使っているモーターや電源の定格電流よりも低い状態で使われていることがほとんどです。
つまり、多くの場合コネクタ選定は使用する機器の定格に合わせて選定していると思いますが、オーバースペックになっている事が多くあります。
代表的な動力源と制御方法についてまとめました。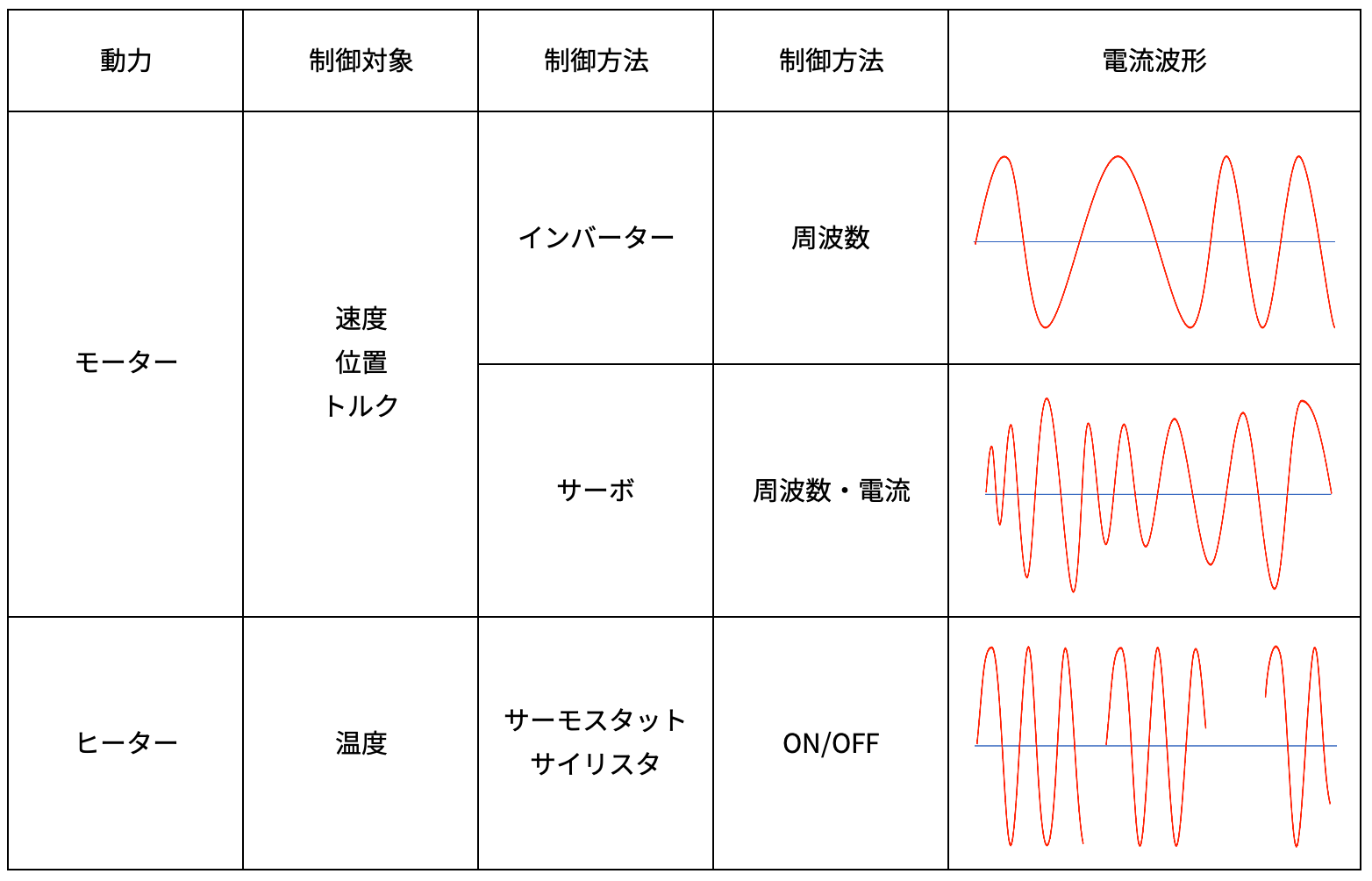
いずれの制御方法も機器定格と実効値のギャップが期待できますが、特にサーボモーターは電流と周波数の両方を制御しているため、実アプリケーションでは実効値が低くなる傾向にあります。
実際の例を見てみましょう。
これは加工機に使われているサーボモーターの電流波形なのですが、最大値は12.7Aですが、実効電流値は4.05Aと1/3以下となっています。
以上のように、制御システムで使われている動力では、機器定格と実効値の差がある場合も多く、慎重に検討を行うことで小さい定格電流値のコネクタを選定することが可能です。
次回は実際のコネクタ選定の方法について解説します。